气体腔频谱感知机理

基于EIT-AT效应构成的里德堡原子射频传感器，其核心在于利用里德堡原子的特殊能级性质：其对微波的响应由固定的物理参数决定，因此可以理论推导出探测微波的频率和强度等信息。

能级跃迁理论

能级跃迁理论是理解EIT效应、认识里德堡原子频谱感知的基础（来源：能级跃迁）

E1跃迁是电场偶极近似（Eletric dipole approximation），假定的是一个均匀的震荡电场的条件下，单光子作用下的跃迁；也是电场对原子作用的0阶近似（在空间上）。E 代表电场，1 代表偶极近似。

E2跃迁是电场电四极矩近似，在更为细致地考虑原子尺度内电场变化时引入，可以合理认为电四极矩都等价于双光子跃迁（考虑一个光子带1份角动量）。

  • E2跃迁的概率要远低于E1跃迁，这是因为E2是更细致的小量
  • 因此E2跃迁常常出现在E1跃迁被禁止的情况。
  • E2跃迁态相较于其他态具有非常长的寿命(ms级)

M1跃迁是磁场偶极近似，在外磁场作用下发生。由M1跃迁的选择定则可以发现：超精细结构中的跃迁是M1跃迁，受到外磁场的驱动。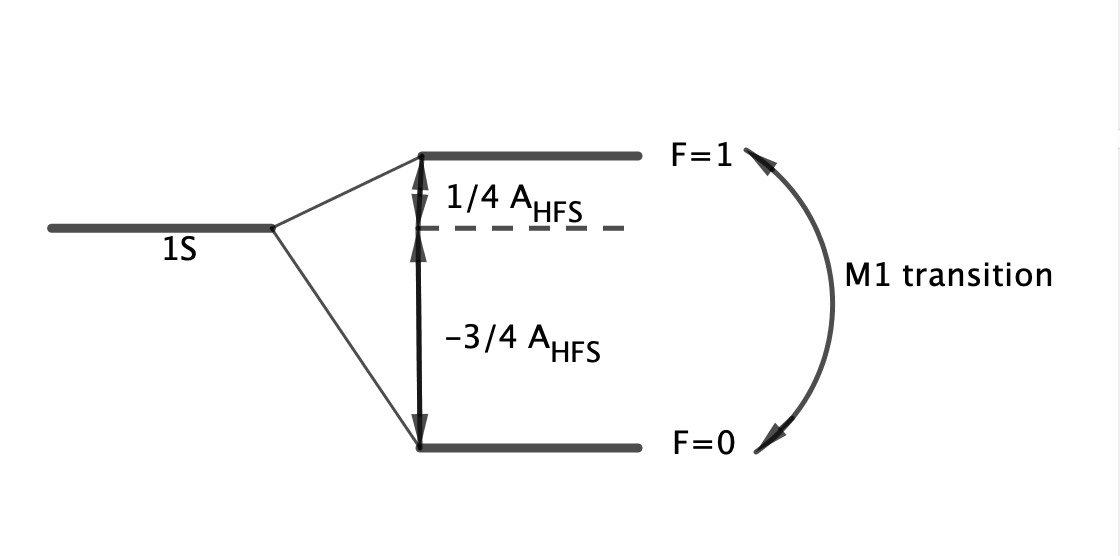

EIT气室频谱感知的物理本质



现在我们可以清楚的是：

  1. 探测光使原子从S态经E1跃迁至P态
  2. 耦合光在扫频至特定频点时使原子从P态经E1跃迁至D态
  3. D态跃迁至S态为E2跃迁过程，其发生相对E1而言非常困难
    • 根据电偶极跃迁选择定则，原子通过双光子激发的方式智能被激发到S或D态[5]
    • 单光子激发方式可以研究P态里德堡原子的相关物理特性，并且受限于紫外激光的功率，目前采用单光子激光制备里德堡原子的研究较少[5]

所以当探测光和特定频点的耦合光对原子气室进行持续的足够强度照射时，绝大部分原子在P态和D态间反复，从而原子气室对探测光诱导透明

此外我们还可以清楚的是：我们关心的里德堡原子频谱感知，其底层物理机制为原子能级M1跃迁

EIT气室原子选择

在绝大多数的文献实验中，原子气室选择了碱金属原子(尤其是其中的铷和铯原子)

碱金属最外层只有一个电子，能级构成相对简单，各种性质也被研究的比较透彻，其可看成由远离核的高激发态电子和剩下来的原子实两部分组成，并能借由氢原子能级导出里德堡激发态能级公式[1]
在精细结构中，碱金属原子最外层电子的自旋角动量S与轨道角动量L耦合为其角动量J(J=1/2、3/2)。考虑原子核的自旋后，出现超精细分裂[3]
根据中心力场近似，可以很好地描述最外层只有一个电子的原子能级结构[6]

铷原子具有研究透彻的超精细结构，对应着可被运用的超精细能级[3]
铷是一种性质极为活泼的金属，87Rb的化学性质相较于85Rb更加活泼，在室温下容易蒸发，且它的吸收光波段使用激光器实现较为简单，并对外加的微波场非常敏感，当有激光作用时会产生显著的光学效应[10]
铷原子的超精细分裂与精细分裂相比虽然小很多，但依然可以分辨。两种同位素的超精细结构如下图所示，根据选择定则，两种同位素的D1线和D2线的超精细分裂分别有4条和6条[3]

铯原子容易被外场激发且能级宽度较窄。以铯原子体系总角动量F=4为例，根据量子力学中的跃迁选择定则，统计从基态能级6S1/2(F=4)到里德堡态200F7/2(F=4)之间所有F=4的超精细能级间的跃迁频率，并将得到的2336组Δf≤40GHz的组合按军用雷达波段划分，计算不同频率带宽下，各雷达波段占空比分布情况：[6]


气体腔参数对里德堡频谱感知性能的影响及气体腔改良

(精细结构)吸收光谱谱线的展宽受到多普勒展宽、功率展宽、压力展宽/平移的影响[7]
对环境因素、温度、激光功率、非线性效应、原子气室(电磁)扰动(气室内部驻波)、阻抗匹配等多个因素进行系统性分析，计算出微波功率测量不确定度[10]

在热平衡时，粒子的速度分布呈高斯分布，多普勒展宽半高全宽宽度与热力学温度存在如下解析关系，式中kＢ为玻尔兹曼常数；Ｔ为热力学温度；ｍ为特征粒子的质量；ｃ为真空光速。此原理已被应用于原级测温。[7]

随着气室周围的温度逐渐升高，气室内部的气压也在逐渐增大，原子间的碰撞加剧导致高能级原子寿命缩短，跃迁过程中断，跃迁时间减小，能级变宽。由于碰撞展宽导致谱线宽度△vc不断增加。[10]
温度对于实验结果的影响主要体现为温度对EIT信号的峰高和线宽的影响导致实验测量结果的波动。EIT信号的峰高越高，信号的强度越大，线宽越小，测量的灵敏度越高，因此为了得到更好的实验测量结果，希望测量到的EIT信号的峰高越高越好，同时线宽越窄越好，然而实验测量结果显示，温度对EIT信号峰高和线宽影响的趋势并不相同，当达到一定温度时，EII信号的峰高随温度的升高而降低。[10]

原子气室的驻波和电场散射效应会对实验测量结果产生较大的影响，本文设计了新型原子气室(材料、结构等)来降低原子气室的影响[10]
原子气室是决定测量准确性的重要因素之一,射频电场可以被原子气室的壁吸收或反射,尽管我们可以通过选择合适的材料来减小反射和吸收，但射频电场的变化可能是由于法布里·珀罗(FP)效应引起的，当射频电场通过气室与原子相互作用时，气室表面的吸收，以及电场与介电材料之间的相互作用，会导致气室内部产生极化效应，当微波入射到气室中，由于玻璃壁的反射，在原子气室内会产生驻波，形成FP腔，产生FP效应。原子气室内部电场分布会根据射频电场的频率与原子气室的大小而发生变化，导致气室内部的电场与入射徼波电场会有差异。Holloway教授团队对原子气室对微波电场扰动的影响及优化方法进行了详细的研究。为了降低扰动，应尽量选用低介电常数的材料来制作尽可能薄的原子气室，且需要减小原子气室的尺寸[10]

在实验中发现有较强的背景噪声对实验测量产生影响，在后续的实验中通过搭建差分探测光路(光路优化)来减小背景噪声[10]

基于量子体系的微波测量,一般采用由石英或者派莱克斯耐高温材料制成的原子气室作为测量探头，以此来降低电磁热效应的影响,传统的微波探头中通常带有电子元器件，电子元器件在受热或强电磁场的作用 下会产生不可逆的漂移，导电元器件在KV/m的场强下其机械结构可能会产生形变或电磁性能的改变等。为了降低电磁热效应的影响，目前实验室常用的由石英玻璃制成原子气室,其介电材料在高达 MV/m的场强下才会发生离子化，因此结构相对稳定，测量结果更加的准确。原子气室由于复杂的结构，特殊的介电性质等因素的影响，实验时需要对原子气室的性能进行分析[10]

为克服温度、碰撞展宽等不良影响，可采用以下机制

  • 冷原子机理[11]
  • 缓冲气体[3]
  • 高真空气室[10]

里德堡频谱感知的性能优势

经典微波电场传感方案局限

目前来说，对于电场的测量手段主要分为三种：利用热电偶效应进行电场测量的热电偶传感器；基于Pockels电光效应完成电场对光场的控制的电场测量系统，从而测量出相应光强与装置晶体端的电压的函数特性曲线；二极管检波（加载偶极子的方式）[2]
然而直到现在，建立一种自动校准 探头来实现这些电场值的独立和绝对测量仍然是一份十分困难的工作。现阶段的微波电场测量标准均是通过“标准场”方法，即通过一个标准天线来测量待测电场，通过这种方式进行探测器的校准。[2]
传统的微波电场探测器存在以下瓶颈：(1)由尺寸限制无法实现高分辨率高灵敏度的电场测量；(2)电场测量溯源链冗余复杂，无法直接溯源至国际单位制SI；(3)探测器的振子本身为金属元件，可能会对待测场产生干扰。同时，随着新兴技术的发展，传统的电场测量方式已经无法满足在chip-on-cell级电磁干扰测量、生物电磁效应感知、微波毫米波近场扫描等需求，可溯源的便携式电场测量设备成为电磁学发展中的主要问题，我们亟需一种新的测量方式来实现对电场的高灵敏度、高准确率和高分辨率的测量，搭建一个完整的测量体系，形成可信赖的有效测量方式，具有可溯源至国际单位制SI的能力，迎合国际发展，提高长期可靠性和对未来的适应性。[2]
经典微波电场传感方案基于金属偶极子天线在微波电场作用下产生感应电流，通过感应电流的测量获得微波电场的振幅、频率、相位等参数信息。其测量灵敏度主要受限于热噪声 (信号和噪声都被编码在电子的宏观运动中)。同时天线尺寸 决定了宏观电流运动的边界条件，影响了微波电场感应驻波电流的建立，进而影响微波测量的灵敏度和带宽。另外传统天线产生的感应电场对被测微波场扰动较大 ，不利于高精度测量的实现。[13]
基于金属天线的传统微波测量(偶极天线)特点为：[14]

  1. 传感器部分(金属天线中的自由电子通过电(磁)偶极相互作用分别响应微波电磁场的电(磁)场分量,从而形成可被测量的宏观运动电流,实现传感功能)
  2. 物理测量部分(将不可直接测量的微波电场转换为可直接测量的物理量)，主要有宽带微波频率计，超外差接收机
  3. 受限于Johnson-Nyquist噪声：在热平衡状态下由于电导体内部的电荷载流子(通常是电子)随机热运动产生的电流噪声
  4. 想获得实际测量灵敏度,要考虑天线尺寸效应，即考虑天线对空间电磁波信号的转化效率
  5. 天线的形状、电偶极天线和磁偶极天线的种类不同、微波频率不同都会影响辐射效率,使得辐射效率难以精确估计和测量
  6. 天线本身的金属结构也会对待测的微波场产生严重的干扰

里德堡原子传感方案优势

里德堡原子频谱感知性能提升的机制优势：[14]

  1. 电偶极矩大，对外部电磁场十分敏感不会强烈吸收电磁波能量
  2. 理论极限灵敏度仅受限于量子投影噪声，远优于传统的微波测量系统
  3. 里德堡激光系统的大连续无跳模扫描范围以及可实现任意里德堡态激发的优势
  4. 原子本身是足够干净的，没有噪声的，足以实现单光子量级的极其灵敏的微波测量
  5. 原子系统也比经典的微波电场计更加直接，原子系统的测量部分仅涉及到微波电场拉比频率的测量,其本质是光学频率的测量。而光学频率的测量是公认的人们目前所能测量理量中最为精确的
  6. 在原子测量系统中，可溯源到普朗克常量、可精确计算的跃迁偶极距、仅涉及到精确的光学频率测量以及原子自身所具有的稳定的特性,使得原子电场计极有可能成为像原子钟一样的新一代微波电场计量标准
  7. 在电极小情况下，原子微波电场传感器可以有效克服天线尺寸效应，避免Chu-Harrington极限

基于EIT光谱技术的里德堡原子电场计：探测灵敏度3mV·m-1·Hz-1/2；场强大于0.3V·m-1时具有较好线性度[13]

缀饰微波场的加入，极大地提高了里德堡原子系综对微波场响应的内禀增益[13]

缀饰里德堡原子超外差接收机：探测灵敏度5.5μV·m-1·Hz-1/2；最小探测微波场强780pV·cm-1[13][14]

考虑到缀饰里德堡原子超外差接收机在被测微波场的强度和本振微波场强度接近时才开始出现非线性效应，表明其线性动态范围可以达到90dB，优于原子电场计约60dB[13]

天线接收提高里德堡频谱感知性能的可行性

传统超外差接收机和里德堡频谱感知灵敏度对比

如果天线指向深空，其等效噪声温度等于宇宙背景辐射的噪声温度，约为Teff=3K，对应于噪声功率密度为－194dBm/Hz。对于有源器件如微波低噪放，其等效噪声温度约等于物理温度，在室温下(T=300K)噪声功率密度为－174dBm/Hz。因此目前传统超外差接收机的理论功率测量灵敏度为－174dBm/Hz。然而在实际情况中，后路的器件依旧会导致额外的噪声，其大小以噪声指数来描述，对于非理想情况下的超外差接收机系统，其噪声指数一般为10dB，即其实际功率测量灵敏度约为－164dBm/Hz。[9]
量子系统的测量灵敏度由海森堡不确定关系和量子噪声极限决定(简称量子噪声)，里德堡原子－量子超外差系统的灵敏度的理论极限用下式表示:

其中，Emin为最小可测量的电场强度，tm为实际测量的总时间，μr为里德堡原子跃迁偶极距，Na为参与测量的原子数，τ为系统相干时间。[9]
里德堡原子发生由47D5/2→48P3/2的里德堡态跃迁，跃迁矩阵元为μr=1443.4498ea0，探测激光功率5μW，参与测量原子数约为106个，系统相干时间20.16ns，原子蒸汽池长度5cm，光斑半径0.85mm，理论极限0.53nV/cm·Hz1/2，折合功率谱密度7.45·10－19mW/cm2·Hz，折合功率灵敏度为－182dBm/Hz，比实际情况下传统的微波超外差接收机差一个数量级，体现出量子测量系统的极大潜力。[9]
基于原子的量子测量体系用一台接收机可覆盖宽频谱，且尺寸可做得很小，突破了传统电磁信号接收天线的尺寸的限制，具有小型化、集成化的优势，在单兵信息装备的配置和使用、无人化平台等方面极具潜力。基于原子传感器的电磁探测，在强电磁辐射情况下仍然可以正常使用，能有效抵抗传统接收机的电磁损伤，同时原子传感器不像传统天线会强烈吸收电磁波能量，使用更灵活和隐蔽，可以提升装备在复杂电磁环境下的生存能力，发挥作战效能，在系统形态、灵敏度和测量精度等方面全面提升电子战系统能力。[9]

参考文献

[1]基于里德堡原子的光子操控于溢琛
[2]基于量子效应的全光学空间电场测量及原子通信接收机研究邹海洋
[3]铷原子D1、D2线的光谱分析与展宽机制杨静
[4]基于里德堡原子的单频微波电场测量陈庆庆
[5]采用319纳米紫外激光对铯…的单光子跃迁里德堡激发研究白建东
[6]基于原子传感器的无源侦察方法研究蒲泳庄
[7]基于铯133原子D1线直接…的多普勒展宽热力学温度测量廖文汉
[8]里德堡原子射频传感器的研究综述王时佳
[9]基于原子传感器的电磁信息感知测量鲜佩
[10]基于里德堡原子的微波功率精密测量张杰
[11]简并费米气体中自旋张量—动…以及里德堡激发态的实验研究李东豪
[12]D.A.Stock.Cesium D Line Data.2010
[13]基于里德堡原子的微波电场量子传感张临杰
[14]基于里德堡原子的微波超外差精密测量研究_景明勇